Posts Tagged ‘BINUS’

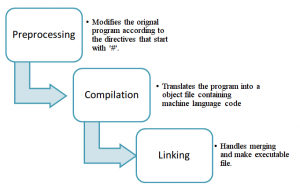
Compilation Process Steps

Compilation is the process of translate our code (source language) into an object file/code that contain computer language (target language).

The overall of compilation processFig 1. Compiler

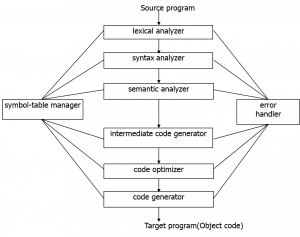
Compiler phasesFig 2. Compiler Phases

A compiler is the program that run the compilation processes. These processes are divided into 2 main phases which are:

A. Analysis Phase (Front-End)

  • The analysis phase will break up the source program into several pieces and imposes a grammatical structure on them. It then uses these structures to create an intermediate representation of the source program. If the analysis phases find some error or ill-formed structures or representation, it will notify the user using some informative message so that the user will know the problem and might take some action to correct it. On this phase, it also collects information about the source code and stores them in a data structure called a symbol table, which is passed along with the intermediate representation to the synthesis part.
  • This phase includes :
    1. Lexical Analysis
    2. Syntax Analysis
    3. Semantic Analysis

B. Synthesis Phase (Back-End)

  • On this part, it will constructs target program based from the intermediate representation and the information in the symbol table
  • This phase includes:
    1. Intermediate Code Generator
    2. Code Optimization
    3. Code Generation

For further understanding regarding each step from both of the phases above, followings are the explanation of each of them.

  1. Lexical Analysis (Scanning)

–    This lexical analyzer reads the stream of characters making up the source program and groups the characters into meaningful sequences called lexemes. From that, it will produces as token. This token will be passed to the next step which is the syntax analysis. The output token from the lexical analyzer will be :

<token-name, attribute-value>

    • token-name = abstract symbol that is used during syntax analysis
    • attribute-value = points to an entry in the symbol table for the token.

For example :

position = initial + rate * 60

  1. position is a lexeme that would be mapped into a token {id, 1 ), where id is an abstract symbol standing for identifier and 1 points to the symbol table entry for position. The symbol-table entry for an identifier holds information about the identifier, such as its name and type.
  2. The assignment symbol = is a lexeme that is mapped into the token {=). Since this token needs no attribute-value, we have omitted the second component . We could have used any abstract symbol such as assign for the token-name , but for notational convenience we have chosen to use the lexeme itself as the name of the abstract symbol.
  3. initial is a lexeme that is mapped into the token (id, 2 ) , where 2 points to the symbol-table entry for initial.
  4. + is a lexeme that is mapped into the token (+).
  5. rate is a lexeme that is mapped into the token ( id, 3 ) , where 3 points to the symbol-table entry for rate.
  6. * is a lexeme that is mapped into the token (* ) .
  7. 60 is a lexeme that is mapped into the token (60) .

The final representation of the statement will be :

<id,1> <=> <id,2> <+> <id,3> <*>

  1. Syntax Analysis (Parsing)

In this step, the parser uses the first components of tokens produced by the lexical analyzer to create a tree-like intermediate representation that depicts the grammatical structure of the token stream.  A syntax tree for the token stream is shown as the output of the syntactic analyzer in the last image of this post.  The subsequent phases of the compiler use the grammatical structure to help analyze the source program and generate the target program.

  1. Semantic Analysis

In this semantic analyzer, it uses the syntax tree created by the syntax analyzer and the information from the symbol table to check the source program for semantic consistency with the language definition. It also gathers type information and saves it in the syntax-tree or the symbol table for intermediate-code generation use.

One of the important part of semantic analysis is type-checking, where the compiler checks that each operator has matching operands. The language specification may permit some type conversions called coercions. If the operator is applied to a floating-point number and an integer, the compiler may convert or coerce the integer into a floating-point number.

  1. Intermediate Code Generation

In this process of translating a source program into target code, a compiler may construct one or more intermediate representations, which can have a variety of forms. Syntax trees are a form of intermediate representation; they are commonly used during syntax and semantic analysis. After syntax and semantic analysis of the source program, many compilers generate an explicit low-level or machine-like intermediate representation, which we can think of as a program for an abstract machine. This intermediate representation should have two important properties: it should be easy to produce and it should be easy to translate into the target machine. We consider an intermediate form called three-address code,which consists of a sequence of assembly-like instructions with three operands per instruction. Each operand can act like a register. The output of the intermediate code generator consists of the three-address code sequence :

tl = inttofloat (60)
t2 = id3 * t l
t3 = id2 + t2
idl = t3

There are several points worth noting about three-address instructions. First, each three-address assignment instruction has at most one operator on the right side. Thus, these instructions fix the order in which operations are to be done; the multiplication precedes the addition in the source program. Second, the compiler must generate a temporary name to hold the value computed by a three-address instruction. Third, some “three-address instructions” like the first and last in the sequence, above, have fewer than three operands.

  1. Code Optimization

The machine-independent code-optimization phase attempts to improve the intermediate code so that better target code will result. Usually better means faster, but other objectives may be desired, such as shorter code, or target code that consumes less power. For example, a straightforward algorithm generates the intermediate code, using an instruction for each operator in the tree representation that comes from the semantic analyzer. A simple intermediate code generation algorithm followed by code optimization is a reasonable way to generate good target code. The optimizer can deduce that the conversion of 60 from integer to floating point can be done once and for all at compile time, so the inttofloat operation can be eliminated by replacing the integer 60 by the floating-point number 60.0. Moreover, t3 is used only once to transmit its value to id1 so the optimizer can transform into the shorter sequence

t1 = id3 * 60 . 0

id1 = id2 + t 1

There is a great variation in the amount of code optimization different compilers perform. In those that do the most, the so-called “optimizing compilers,” a significant amount of time is spent on this phase. There are simple optimizations that significantly improve the running time of the target program without slowing down compilation too much.

  1. Code Generation

The code generator takes as input the intermediate representation of the source program and maps it into the target language. Then, the intermediate instructions are translated into sequences of machine instructions that perform the same task. The crucial aspect of code generation is the judicious assignment of registers to hold variables.

For example, using register R1 and R2, the intermediate code will get translated into the machine code :

LDF R2 , id3
MULF R2 , R2 , #60 . 0
LDF R1 , id2
ADDF R1 , R 1 , R2
STF id1 , R1

  • The first operand of each instruction specifies a destination.
  • F in each instruction tells us that it deals with the floating-point numbers
  • # signifies that 60.0 is to be treated as an immediate constant.

Explanation:

1. id3 is load into the R2 register
2. the value in R2 is being multiplied by 60.0 and stores it into R2
3. id2 is load into the R3 register
4. add the value of R2 with R1 and stores the result into R1
5. Store the value of R1 into id1 (assignment)

The processes of all above are shown in following picture:

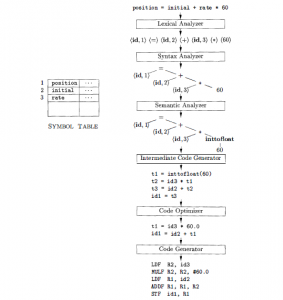lexical analyzer processFig 6.1 Translation of assignment process

References :

BINUS University

Tags: , , , , , , , ,

Technics Compiler Comments 0 Mar 16th, 2014